Toys' Cafe
Show canned hints
Hints reveal on hover.
| Keywords | Hint |
|---|---|
| start | One of the toys in this puzzle is a 5-disc Towers of Hanoi. How many different states can you put that toy in? The internet has more info about this particular graph. |
| snake, blocks, chess | Snake: If the snake chases its own tail in a loop, then it will slither around the same size loop in the graph. Can you ID the two loops the red state lives in?Blocks: The blue state is in a long road of unique moves. At the end of that road, the Γ-shaped block is in the top-right corner, and the ⌟ block is in the bottom-right corner.Chess: Try to find a configuration where there's only 1 legal move. There are only 2 such configurations, and you can use the red state to disambiguate which is which. |
| water, tic, tac, toe, hanoi | Water pouring: The graph is a total mess. But it's symmetric, and the symmetry maps the red state to the blue state. Can you find the symmetry of the water-pouring toy? It's a generic symmetry of water-pouring puzzles: that is, it applies no matter how tall each glass is.Tic-tac-toe: What move must have been played last, and what does the graph tell you about ways O and X could have won earlier? A useful observation: numbering the columns of the graph 0, 1, 2, 3, and 4, there is a vertex in column 2 that leads to two terminal vertices in column 3.Towers of Hanoi: The three corners of this graph are the unique Towers of Hanoi states with only two legal moves. What are those states? If all else fails, you can find info about this particular graph online. |
| extract, extraction | [[If the solvers are stuck here, they probably either (1) have incorrect work, or (2) are staring at a grid with blue cells shaded, instead of thinking about the actual picture. If the latter...]]What does the picture look like when all the toys are in the correct states? I mean the *actual* picture. |
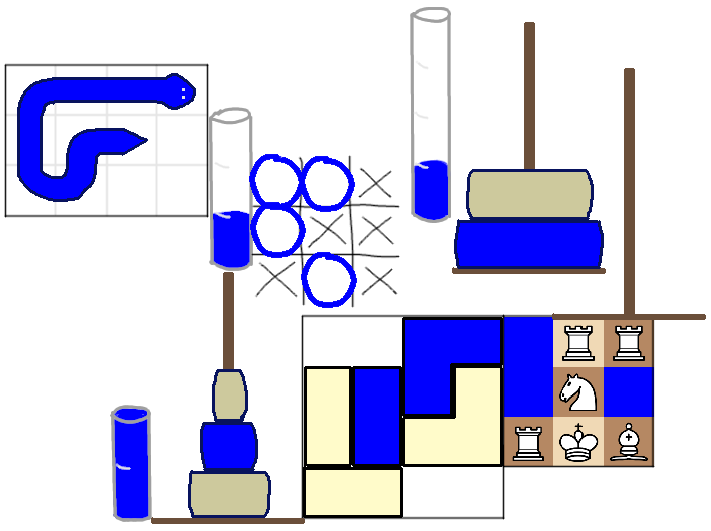
(In case it helps: the graphs have 136, 140, 243, 150, 30, and 54 vertices respectively, and the last graph is rotationally symmetric.)